Background

Collection must be the most commonly used data model in programming. And there are a number of data structure that represents collection in memory, in which Array and Liked List must be the most well known ones.

When dealing with collection, filtering must be one of the most widely used operation being used. Such as find item(s) satisfies specific criteria from the collection. Although filtering is used a lot, but it isn’t actually a simple or easy operation to apply, especially dealing with tremendous data volume.

In fact, there are a number of derived topics about collection filtering, which is impossible to cover them all in the article. This article will focus on bit operation, probably a not widely known but really interesting topic to introduce.

Problem: Find the missing integer

Problem
Suppose there is a collection of integers L.
Name the collection that contains integers from 1 to N as G
Then L contains all the elements of G except one number x.
Items in L are in random order.
Find x.

TIP: This problem be too easy to experienced developers and algorithm hackers. But it is a good opening words to the following 2 problems in this series. Also it reveals the core concept of some other advanced technologies, such as CRC or bloom filter.

When got this problem, the very intuitive(means do it manually by human being) idea is to compare the elements in L and G, find each element in L and remove it from G, then the only left item in G is x.

Here is the code:

1
2
3
4
5
6
7
8
9
10

# @param Integer[] L
# @param Integer N
# @return Integer x
def find_missing_x(L, N)
  G = [*(1..N)] # Create G with all integers from 1 to N
  L.each { |i| G.delete(i) } # Traverse L, and remove each item in L from G
  return G.last # Return the only rest item from G
end

Well this is a work but brute algorithm, which is not efficient in both time and space:

• Instantiate G means it has space complexity N
• Find and remove i from G means it has time complexity at O(N*Log(N))

Yes, the algorithm can be optimized, with bit operation. In fact the problem can be resolved with time complexity O(N) and space complexity O(1).

Exclusive-Or Operation

Exclusive-Or(Or XOR for short, written as ^ in this article) is a basic bit operation, here is an Venn Diagram explains it:

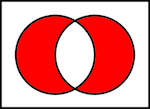
XOR is an important bit operation because it has following interesting features:

1. A ^ B = B ^ A (aka Commutativity)
2. (A ^ B) ^ C = A ^ (B ^ C) (aka Associativity)
3. A ^ A = 0
4. A ^ 0 = A

Commutativity and Associativity ensure that XOR can be used despite of order. The 3rd and 4th feature establishes a critical position for XOR in cryptology and encoding.

Solution: with XOR

By making use of XOR, previous problem can ben resolved in a much more graceful way:

• Given y is the xor result of all items in G
• And z is the xor result of all items in L
• Then x = y ^ z

1
2
3
4
5
6
7
8
9
10
11
12

# @param Integer[] L
# @param Integer N
# @return Integer x
def find_missing_x(L, N)
  x = 0 # Set x to 0, since A ^ 0 = A
  (1..N).each { |i| x ^= i } # Calculate the xor result for G
  L.each { |i| x ^= i } # Keep xor all elements in L
  return x # Return the only rest item from G
end

Let’s prove it mathematically:

1
2
3
4
5
6
7

Given x'= y ^ z
Then  x' = (n1 ^ n2 ^ n3 ^ ... ^ x ^ ... ^ nN) ^ (n1 ^ n2 ^ n3 ^ ... ^ nN)
Since ^ obeys commutativity and associativity
Then  = (n1 ^ n1) ^ (n2 ^ n2) ^ ... ^ (nN ^ nN) ^ x
As n ^ n = 0 and n ^ 0 = n
Then  x'= 0 ^ 0 ^ ... ^ 0 ^ x
         = x

Actually the code can be more concise by using reduce, with 2-lines of code

1
2
3
4
5
6
7
8

# @param Integer[] L
# @param Integer N
# @return Integer x
def find_missing_x(L, N)
  x = (1..N).reduce(&:^) # Calculate the xor result for G
  L.reduce(x, &:^) # Keep xor all elements in L and return
end

Or C version:

1
2
3
4
5
6
7
8
9

int find_missing_x(long N, long* L) {
  long x = N;
  for(long i = 0; i < N - 1; i++) { // L has size of N-1
    x ^= i ^ L[i];
  }
  return x;
}

Extending problems

So far the problem has been gracefully resolved. But it is yet the end, here is a couple of extending questions:

1. If G is collection with random but unique numbers (Not continues integer from 1 to N). How to write the code?
2. Based on 1, if there are 2 numbers are missing? How to find them both?
3. Based on 1, but L contains the members from G except xfor exactly 2 times. That means L might contain 0 or 1 x, but exactly 2 for any other members from G. How to find x?
4. Based on 1, but G isn’t a collection of integer, but a collection of web urls. How to find the one missing url?
5. Based on 4, G is a collection of url, L is subset of G (might contains fewer members other than exactly N - 1). How can we know a randomly picked member from G is absolutely not contained by L. Given the tolerance to mistake on saying a member from G is in L but it doesn’t.

These problems will be explained in the following posts.

To test the the exception in a rejected promise could be a little bit painful.

And Mocha is Promise-friendly, which means it fails the test if exception is not caught.

So as a result, here is a simple code example to explain how it is being done:

1
2
3
4
5
6
7
8
9

it 'should throw session-expired exception'
  new Session().generateId().bindUserFromRedis()
  .then ->
    null
  .catch (ex) ->
    ex
  .then (ex) ->
    expect(ex).to.be.instanceof(ResponseError)
              .and.that.have.property('errorName', 'session-expired')

Update: A Chai Plugin can mitigate the pain

1
2
3
4
5

it('should throw session-expired exception', () => {
  return expect(new Session().generateId().bindUserFromRedis())
           .to.evetually.rejected
              .and.that.have.property('errorName', 'session-expired')
})

Update 2: With async, it can be converted into normal test

1
2
3
4
5

it('should throw session-expired exception', () => {
  return expect(async () => await new Session().generateId().bindUserFromRedis())
          .to.throw
             .and.that.have.property('errorName', 'session-expired')
})

EventBus is an special Publish & Subscribe Pattern implementation. EventBus enable message to be delivered between components without requiring the components to register itself to others.

Comparing EventBus to other Pub & Sub implementations, EventBus is:

1. Designed to replace the original event distribution system, which requires the components register itself to each other.
2. Not designed for general use, EventBus adds additional complexity and runtime overhead to the system. So it is not designed to replace normal method calls.
3. Not designed for inter-process communication as some other Pub&Sub.

EventBus saves Android developers’ life

When developing Android application, I strongly recommend developer to introduce an EventBus library. EventBus from GreenRobot, Otto from Squqre are good solutions. Or even to choose the original EventBus in Guava library from Google.

With EventBus, components can communicate with each other without need to hold direct reference of each other. This is very important to avoid app crashes when calling a method on a detached or destroyed component. Usually this kind of issue isn’t that easy to handle due to Android’s over-complicated life cycle management. So even in the worst case that one component is sending message to another component which has been destroyed (which should unregister itself from EventBus on that time), it only triggered a norecipient waring instead of crashing the app.

Also with EventBus as intermedia, you can avoid to exposing objects to root activity or application just for registering callbacks on each other. Components are higher cohesion & lower coupling.

As the result, EventBus saves tons of time to debugging crash, and make your code more readable, maintainble, extensible, and flexible.

Abusing EventBus kills your app easily

“EventBus is awesome! It is so convenient, so let’s replace everything with event”… This kind of saying is commonly heard from the developers who just realized the benefits from EventBus. Since EventBus is too convenient to use, they tends to replace everything with EventBus.

But we mentioned in the introduction of EventBus that EventBus is design to replace traditional event system in Java, and is not designed for general use. Abusing makes your code hard to understand, hard to debug. Long event chain is a common reason that cause of unexpected behavior.

Broadcast Event, Command and Request

EventBus is powerful, but can be easily abused. To make a better use of EventBus, I learn a number of EventBus usages, and evaluated the scenario, and summarized out 3 typeical EventBus usage patterns: Broadcast Event, Command and Request.

Broadcast Event

Broadcast Event is a special kind of event that used by a specific component to broadcast its status updated to other components.

Declaration

Broadcast Event should be used when several components cares about the specific component’s status update. So usually Broadcast Event should have more than one recipients or, at least, potential recipients.

Broadcast Event should be an immutable data object, so:

1. It is immutable, so once it is created, its status should not changed, which guarantees the equality between recipients.
2. It is data object, so it should not has methods that might change other classes status.
3. It might have methods that helps its consumer to consume the data it contains.
4. It should be declared as a nested static class of publisher.

NOTICE
If you thought a Event is “Broadcast Event”, but later you found it has only one recipient, then you might need to consider refact it into a Command or a Request.

Command

Command is a special kind of event that has the ability to update specific object or specific type of objects. In most cases, Command should have only one recipient. In some special cases, it might has a group of recipients with exactly same type.

Precisely, the latter case is a variant of Command pattern, Batch Command, which works as same as Command but have multiple recipients so it can update multiple instances in a batch.

Command should be a immutable object that able to update specific object, so:

1. It should have 1 execute method with 1 parameter, which represents the target that the command updates.
2. When invoking execute method shouldn’t change its own status, so it does exactly same thing when applying it to multiple targets.
3. It behavior should be stable across time, so its behavior won’t change when it is apply asynchronously.
4. The object that execute method accepts is not necessarily to be the recipient. It could be the object that recipient holds or it has access to.
5. It should be declared as nested static class of the recipient.
6. If recipient accepts multiple events, these events are recommended to derived from the same base class. So The recipient could subscribe to the base class, rather than every command.

NOTICE
Command can be seen as recipient’s special method that can be invoked without known recipient instance. So its behavior should fully contained in the class. The subscribing method on recipient should contain one line of code to invoke execute method on command.

Request

Request is a special kind of event that has the ability to accept data from another object. If the request has multiple recipients, to avoid ambiguous behavior, there should be only one of Request‘s respond the request.

But there is one exception, that is for the request collects data from multiple objects, multiple objects might respond to the request. This special kind of Request is called Collector.

Request should be a object that accept data from recipient, so:

1. It should have respond method with 1 parameter, which represents the data the request asks for.
2. Request should contains enough information for the recipients to determine whether to respond the request.
3. The recipients should check request’s status to determine whether it should respond request.
4. The request can update the publisher directly in the respond method
5. It should be declared as nested class of publisher. If possible, also declare it as static, which will be helpful to simplify the tests.
6. Request might has methods to help recipient to determine whether to respond the request.

NOTICE
Request can be seen as a special method that publisher exposes to a specific recipient, so the specific recipient can invoke the method to provide data. For Request, you might need to aware that that sometimes request might not found proper recipient to respond. If the responder is not guaranteed to exist, then the publish to watch out no-recipent warning from EventBus.

• Part 1: What it is for and how to used it

In android, view hierarchy usually are created via layout xml file. In the file, to instantiate a TextView we write:

1
2
3
4

<TextView
    android:layout_width="wrap_content"
    android:layout_height="wrap_content"
    android:text="Sample 1" />

Usually, we need to specify the visual of the TextView, so we keep adding attributes to the TextView element:

1
2
3
4
5
6
7
8
9
10
11
12

<TextView
    android:layout_width="wrap_content"
    android:layout_height="wrap_content"
    android:text="Sample 1"
    android:background="@drawable/category_indicator_background"
    android:gravity="center"
    android:maxLines="1"
    android:paddingBottom="12dp"
    android:paddingLeft="22dp"
    android:paddingRight="22dp"
    android:paddingTop="12dp"
    android:textSize="12sp" />

Usually to fully customize visual representation of a view needs a lot of attributes and resources. Such as in this example. we added background, gravity, maxLines, padding and textSize, which is a lot of code.

And if we want to create another TextView with exactly same visual representation, we need to copy all the values again:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

<TextView
    android:layout_width="wrap_content"
    android:layout_height="wrap_content"
    android:text="Sample 1"
    android:background="@drawable/category_indicator_background"
    android:gravity="center"
    android:maxLines="1"
    android:paddingBottom="12dp"
    android:paddingLeft="22dp"
    android:paddingRight="22dp"
    android:paddingTop="12dp"
    android:textSize="12sp" />
<TextView
    android:layout_width="wrap_content"
    android:layout_height="wrap_content"
    android:text="Sample 2"
    android:background="@drawable/category_indicator_background"
    android:gravity="center"
    android:maxLines="1"
    android:paddingBottom="12dp"
    android:paddingLeft="22dp"
    android:paddingRight="22dp"
    android:paddingTop="12dp"
    android:textSize="12sp" />

Obviously, in this piece of code, there are a lot of duplications. We need to compare all the values to figure out the 2 TextViews have the same visual. If we want to change the style, we need to update 2 TextViews. And the last, if we want to create the 3rd TextView or even more ones, we need copy the code again and again, which makes the issue become more troublsome.

In a short word, the code has bad readability, bad maintainability, bad reusability. In the book Refactor, we know that code redundancy is bad smell. To mitigate the issue, we need to extract the shared code into another “unit”, and replace all the occurrences with the reference.

In Android layout xml, the extract “unit”, which represents the shared attributes, are called Style. After introduced Style, we have:

1
2
3
4
5
6
7
8
9
10
11

<TextView
    android:layout_width="wrap_content"
    android:layout_height="wrap_content"
    android:text="Sample 1"
    style="@style/TextView.Customized"/>
<TextView
    android:layout_width="wrap_content"
    android:layout_height="wrap_content"
    android:text="Sample 2"
    style="@style/TextView.Customized"/>

1
2
3
4
5
6
7
8
9
10
11
12
13

<resources>
    <style name="TextView.Customized">
        <item name="android:gravity">center</item>
        <item name="android:background">@drawable/category_indicator_background</item>
        <item name="android:paddingLeft">22dp</item>
        <item name="android:paddingRight">22dp</item>
        <item name="android:paddingTop">12dp</item>
        <item name="android:paddingBottom">12dp</item>
        <item name="android:textAppearance">@style/CategoryIndicator.Text</item>
        <item name="android:textSize">12sp</item>
        <item name="android:maxLines">1</item>
    </style>
</resources>

Well, this is the basics about the Style: why we need it and how it is used.

This post is Walkthrough to the game Untrusted
The game introduction is available here: Awesome geek game Untrusted

Level 1: cellBlockA

Well, you are trapped in a box. And you need to move yourself to the exit (blue squre).

1. Before you can do anything, you need to pick the computer first, then you will be access to the source code interface.
2. Once you got the computer, you can figure out the code that generates the walls.
3. Remove the code that generate the wall! And press Ctrl+5 to apply it.

Level 2: theLongWayOut

Well, you have learn the trick from Level 1, but it doesn’t work anylonger this time. You need to figure out a new apporach.

1. Don’t try to find a path in the maze, there is no such solution.
2. You cannot change the maze created, but you can do something to it before it is deployed.
3. You have learn how to create it for specific size. Why not create another smaller one that doesn’t trouble you?!
4. A maze with size (0,0) is not possible, try a more realistic one, such as (3, 3) or (4, 4).
5. Exit is blocked completely. Do think about to break the wall, that is impossible.
6. Who said there can be only 1 exit per level?!
7. Create a new exit at a different location! You can learn the code form existing one.

Level 3: validationEngaged

Well, again, validateLevel is introduced, which prevents you to replay the old tricks. So you cannot create or remove objects on the fly this time.

1. Since you cannot create or remove objects this time, but you still can move objects.
2. Move one of the wall away to make a gap between the wall.

Level 4: multiplicity

You cannot move wall this time, what will you do?

1. Well, this is just a mindset trap. Forget about moving stuff aroud.
2. There is no validateLevel in this level.
3. What you did in level 2.
4. Just create a exit in the box.

Level 5: minesweeper

Remember the favous game in Windows? Try it here.

1. The issue here is that the mine cannot be distinguished.
2. Mark the mine with a color other than red.
3. You can change block block color by call setSquareColor.

Level 6: drones101

A killing drone? Keep away from it.

1. Well, check moveToward, the logic is actually very dumb.
2. It always, move up and down if the x offset is larger than y offset.
3. It will not move, it the intented direction is blocked.
5. Move right first, then move down when you at the same col as the drone and block. Then move right, the drone will not follow you.

Level 7: colors

A phone to make call? Great idea!

1. Pick up the phone, then press q
2. The callback will be executed everytime you pressed q
3. Rotate your color in the callback

Level 8: intoTheWoods

Go across the forest from the left to the right!
In this level, there is very little code that you can change!

1. Press q
2. The only code you can change is the callback function name
3. All the functions that you can call are in the functionList
4. Generate a new forest, when you press q
6. Move right as far as you can; Once you are blocked, press q to generate a new forest, the move.
7. Repeat move and generate forest untill you reach the exit.

Level 9: fordingTheRiver

Well, a self driven raft, the raft comes to pick you up.
BTW, I really love the BG music of this level.

1. The raft direction is stored in variable raftDirection.
2. Change the raftDirection to up, will make the raft move up each turn.
3. Find a chance to override the value of raftDirection.
4. Write a function that registerd as phone call back with API setPhoneCallback
6. Go to the raft, after boarding the raft press q to execute callback, then move up.

Level 10: ambush

Well, this time, there are a dozen of drones are on your way. You need to figure out a possible to get rid of them as fast as you can.

1. Don’t try to run away as what you did in Level 6. It is a different scenario.
2. Try to change the drone behavior.
3. To apply the same logic to 3 kinds of drones might not be a good idea.
4. Move attak drones away from the row you’re in.
5. Move the Defence Drones away from the row you’re in.
6. Ask Reinforcement Drones to stay at the place.

Level 11: robot

This time, there is very little thing about you. It is about the robot.

1. “Hit and turn” should be smart enough for the puzzle.
2. Move forward, when hit something, turn 90 deg.
3. Use me.canMove to test the hit.
4. Since there just 2 states, a boolean should be enough to represent the state.

Level 12: robotNav

Well this time, it goes a little complicate.

1. “Hit and turn” won’t work here.
2. Path seeking algorithm is way too complicate for this puzzle.
3. Robot should be able to be “programmed”.
4. An instruction system should be enough for the puzzle.
5. Preset the instruction to the robot, and ask robot to execute it step by step.

Level 13: robotMaze

Well, Well, Well, it upgraded again. More intelligence is needed.

1. Maze is randomly generated, so fixed instruction sequence won’t work any longer.
2. Again, Path seeking algorithm is way too complicate for this puzzle.
3. Don’t waste your intelligence.
4. A lot of robot can be “controlled” remotely.
5. Try to teach the robot how to move by your character’s movement.
7. The robot move down when you’re in last row; the robot move up when you’re in the last 3rd row; the robot try to move to your col when you’re in the last 2nd row.
8. Move into last 2nd row, and the move to most left. Move left and right to control robot move horizontally. Move to last 3rd row or last row when you need to tell robot move up and down.
9. Stay in last row and last 3rd row, and press ‘r’ will move robot up and down continuously.

Level 14: crispsContest

Again another maze!

1. The maze is unsolvable, don’t try to solve it.
2. Divide the maze into 5 regions, top left 2 rooms, top right 2 rooms, left 1 room, right 1 room, and bottom 2 rooms.
3. You can hold only one key for each color, or the key will be wasted
4. Because of restriction(hint.3), left and right regions are meaningless.
5. Region top left, top right, and bottom, enter and exists direction doesn’t matter.
6. Check carefully, a string in the code isn’t locked.
7. The item will be taken away is editable when you pass greenLock.
8. Computer and phone are important items for your further plan.
9. null or undeclared value causes exception.
10. Exception will break the code execution, which blocks you from passing the door.
11. Try to find something exists, but you don’t have yet.
12. The Algorithm ?

Level 15: exceptionalCrossing

Really a cruel design… Pick how to die? Tricky but interesting!

1. The only thing you can change it the value passed to player.killBy().
2. Try to remember what you encounter in last level.
3. Get some hint from the name of this level.
4. Exception breaks code execution.
5. null is a valid value.
6. Undeclared value causes exception.

Level 16: lasers

Lazer kills different races.

NOTICE You might got killed by lazer when you haven’t actually touched it. The reason is that the line isn’t 100% align with the coord is given. And I think it is a BUG than designed by purpose.

1. Lazer representation and collision detection are separated.
2. Remove the drawing logic won’t solve the issue.
3. Lazer only kills the object with different color than itself.
4. Color the lines with the lazer color.
5. Use the phone to update your color.

Level 17: pointers

This must be the most problematic level in the game!!!!
Since fortune is more important than wisdom in this level!
If you’re lucky enough, you might able to clear the level by entering a randomly picked portal.
Actually when I play this level for 1st time, I passed without dohing any code work.

1. Well, you can do nothing to the layout, and teleporter links.
2. A path seeking algorithm won’t be helpful for this puzzle.
3. Not all the layout is solvable. That’s why you need some fortune!
4. You’ll be killed immediately if the teleporter is linked to a trap.
5. Try to figure out all the safe links, whose 2 end-points are teleporters.
6. Try to visualize the the safe links.
7. Check API document for new available APIs.
8. Use map.getCanvasCoords to figure out the plot coords for teleporters.
9. Draw lines between safe teleporters.
10. Line drawing code can be found in previous level.
12. Restart the level, if the level is obviously not solvable.
13. The puzzle is unsolvable, if there is no link to the room where exit locates
14. The puzzle is unsolvable, if there is no link to the room player is placed.
15. Luck is the key!

Level 18: superDrEvalBros

Great honor to Super Bro.Mario 🏆

1. Jump is kind of misleading word.
2. “Bridge” should be a better solution.
3. To material builds the bridge is not necessarily to be “block”.
4. Create your material.

HINT If you really like to jump:

1. Jump is possible, but not a really good solution, since it introduces races between 2 timers.

Level 19: documentObjectMadness

jQuery!!!!

1. Code isn’t editable at all in this level.
2. Use the arrow keys to navigate the green block.
3. You need to use green block to cover the red block.
4. If you familiar with EverNote Web Clipper, then it should be very easy for you.
5. Press up for 4 times, then right 2 times, and adjust your green block to cover red

Level 20: bossFight

Finally, fight against the BOSS!

1. To clear the level, you need to kill all the bosses to get the Algorithm first.
2. Timer is not available.
3. So before you can do anything, you need the phone to trigger something.
4. Only 1 block is available
5. You can place the only block in the middle of the gap to shelter the bullet for you. With its help, it isn’t that hard to get the phone without being shot.
6. Or You might create a new tile to shelter the bullets for you, the number of new material blocks are not limited.
7. To kill the Boss, you need create your own bullet!
8. If you create your own shelter material, you can make it passable for your bullet.
9. Who said the bullet must be shot from your position?
10. Who said the bullet must fly from bottom to top?
11. Who said you can only shot one bullet per key press?

Level 21: endOfTheLine

It is the End?

1. This isn’t really the last level!
2. The key is map.finalLevel = true;.
3. Press Ctrl+0 to check what is inside.
4. What is in scripts/ folder?
5. Why some blocks are purple, some others are black?
6. Check objects.js, find exit object definition.
7. Comment out if (!game.map.finalLevel) { and }
8. Go to next level!

Untrusted is an awesome game brought to us by Alex Nisnevich and Greg Shuflin. Untrusted is an unique puzzle game designed for geeks and developers. The reason I said it is designed for geeks and developer is because to solve the puzzles in the game, you need to know or even to write some javascript.

Here is how the creators describe their baby:

Untrusted —or— the Continuing Adventures of Dr. Eval is an exciting Meta-Javascript Adventure Game wherein you guide the dashing, steadfast Dr. Eval through a mysterious MACHINE CONTINUUM, wherein, using only his trusty computer and the TURING-COMPLETE power of Javascript, he must literally ALTER HIS REALITY in order to find his freedom! You must literally edit and re-execute the very Javascript running the game in your browser to save Dr. Eval from this dark and confusing reality!

The description is a little bit hard to understand if you don’t touch the game. I’ll try to translate it a little bit:

In the game, to clear a level, you need to move your avatar to the exit. And just like other normal acarde game, you can control the your avatar, Dr. Eval using arrow keys. The intresting part of this game is that basically, you will always run into the a dead end if you just move Dr.Eval around without doing anything else. Luckily, you will be able to access the source code that creates the world and the rule in the world. To save yourself from the dead end, you need to change part the world/rule by hacking the source code.

The game isn’t that hard if you have some coding experience and is familiar with javascript concepts. And learn from the passed level is very important, since you might find either useful hints or even code to solve your current problem.

NOTE Besides the puzzle and the code, the music of each level is also great! 8Bit music in different style! Really awesome!

Insterested? Here is the port lead to the game: Untrusted

Hints and Walkthrough

I attached my hints and solutions below, is case if you run into trouble.

I have extract the walkthrough into another post.

Here is the link to the walkthrough: Walkthrough

Robolectric is an awesome library that makes UI unit test on Android a lot easier and faster. In UI test, one of the most basic thing is to simulate user interaction, such as clicking a button.

Click on individual View

Click should be the most basic user interaction, besides invokeing the View.performClick() method, Robolectric provides a more smarter version Robolectric.clickOn(View), which checks the view visibility and enabled status before actually “click” the view. If a view is either not visible or disabled, the click action will not be performed. This mechanism is useful to avoid some silly cases in automated tests.

Long Click on individual View

Long click is a more advanced click action. To simulate a long click action, View.performLongClick() can be invoked. But since Robolectric doesn’t provide any long click helper, make sure you do it by yourself, including checking whether view is long-clickable, which usually will be set manually or more often, when View.setOnLongClickListener is invoked; view is visible and enabled as what click does. Although Long click is avaible to use, but from my experience, long click on a individual view is rarely used in real UI design, instead long click is usually performed on an item of list view or grid view. This is the trickest case that I’ll leave it to the last.

Click on item of List/Grid

Click on List View or Grid View item. Well, idally, this shouldn’t be so much different than click on a indiviual view. But in Android implementation, item click is handled by the list view with a much more complicated API. To perform an item click, boolean performItemClick(View v, int position, long id) can be invoked. performItemClick requires 3 parameters, the first one is the view being clicked, the second one is the position of clicked view’s corresponding data item in adapter and the last is the if of clicked view’s corresponding data item. Complicated, isn’t it?

In Android implementation, item view displayed in ListView/GridView is actually provided by its adapter. Adapter works like a presenter in MVP pattern that creates/update item view based on the item data it holds. It also provides the id for the item. So to perform a item click, besides the ListView/GridView, you also need its adapter.

Following implementation explains how it works:

1
2
3
4
5

public static void clickItem(AbsListView listView, int position) {
    ListAdapter adapter = listView.getAdapter();
    View itemView = adapter.getView(position, null, listView);
    listView.performItemClick(itemView, position, adapter.getItemId(position));
}

In the code, AbsListView is the base class of ListView and GridView. To click the item, you need

1. Get the adapter of the AbsListView
2. Create an item view for specific position with adapter
3. Calculate the item id of corresponding position
4. Invoke performItemClick method with data we got before.

In the implementation, for simplicity reason, we ignored some cases, such as convertView reusing. From my experience, in most cases, it won’t impact the functionality, so we don’t need to worry about it, unless you clearly know that matters, then you need to cover them in your tests.

Long click and item of List/Grid

Well, this action is also not a commonly used. It is only used in limited cases, such as selecting multiple item or displaying context menu for specific item.
To perform a long click on the item is the most trickest case. In previous 3 cases, we either directly or indrectly depends on View.perform***Click method. But not sure why, android doesn’t provide similar public API method of item long click. By diving into Anrdoid source code, we can figure out that Item Long Click isn’t really handled by ListView itself, instead it is handled by a Runnable named CheckForKeyLongPress. To invoke method on this object isn’t that streight forward, and might involes unnecessary multithread issue.

I just want to click a item, why I have to deal with these unnecessary complicates? So I learnt from the CheckForKeyLongPress implementation, and implmented my own “API”:

1
2
3
4
5
6
7
8
9
10
11
12
13
14

public static void longClickItem(AbsListView listView, int position) {
    if (!listView.isLongClickable())
        return;
    OnItemLongClickListener listener = listView.getOnItemLongClickListener();
    if (listener == null)
        return;
    ListAdapter adapter = listView.getAdapter();
    View itemView = adapter.getView(position, null, listView);
    listener.onItemLongClick(listView, itemView, position, adapter.getItemId(position));
    listView.performHapticFeedback(LONG_PRESS);
}

My main purpose of perform a click is to trigger the corresponding listener, so I tried to invoke the listener directly with some necessary pre-checks. This aporach will not triggers these UI effects, but I assume it can meet most test cases.

APPENDIX UIActions helper class

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59

package me.timnew.robolectric.utils;
import android.app.Activity;
import android.app.Fragment;
import android.view.View;
import android.widget.AbsListView;
import android.widget.ListAdapter;
import org.robolectric.Robolectric;
import static android.view.HapticFeedbackConstants.LONG_PRESS;
import static android.widget.AdapterView.OnItemLongClickListener;
public class UiActions {
    public static boolean clickOn(View view) {
        return Robolectric.clickOn(view);
    }
    public static boolean clickOn(Activity activity, int targetViewId) {
        return Robolectric.clickOn(activity.findViewById(targetViewId));
    }
    public static boolean clickOn(View parentView, int targetViewId) {
        return Robolectric.clickOn(parentView.findViewById(targetViewId));
    }
    public static boolean clickOn(Fragment fragment, int targetViewId) {
        //noinspection ConstantConditions
        return Robolectric.clickOn(fragment.getView().findViewById(targetViewId));
    }
    public static void pressBackButton(Activity currentActivity) {
        if (currentActivity.getFragmentManager().getBackStackEntryCount() > 0)
            currentActivity.getFragmentManager().popBackStackImmediate();
        else
            currentActivity.onBackPressed();
    }
    public static void clickItem(AbsListView listView, int position) {
        ListAdapter adapter = listView.getAdapter();
        View itemView = adapter.getView(position, null, listView);
        listView.performItemClick(itemView, position, adapter.getItemId(position));
    }
    public static void longClickItem(AbsListView listView, int position) {
        if (!listView.isLongClickable())
            return;
        OnItemLongClickListener listener = listView.getOnItemLongClickListener();
        if (listener == null)
            return;
        ListAdapter adapter = listView.getAdapter();
        View itemView = adapter.getView(position, null, listView);
        listener.onItemLongClick(listView, itemView, position, adapter.getItemId(position));
        listView.performHapticFeedback(LONG_PRESS);
    }
}

Start a new Android project this week, so I started to setup the development environment. To be honest, it is not an easy experience to me.

Features

Here are the features I got now:

• Unit test with Robolectric. (Very fundamental requirement)
• Unit tests are separated into an independent module. (Provide flexibility when project growing larger. And provide a more clear view of code organization)
• Running unit tests recognized by Android Studio/IntelliJ unit test plugin and debug UTs in IDE. (This is very important when diagnose failure UT)
• Running unit tests via CLI with gradle wrapper. (This is necessary requirement for CI servers)
• Using resources in Robolectric test. (Avoid Resource Not Found exception in unit tests)
• Test Android Annotation powered async implementation. (AA introduces new Async implementation, which is not supported by Robolectric by default)
• AssertJ core support. (Fest has been deprecated since no one is maintain it now.)

Versions

The major difficulties that I met are version compatibility, I almost tried all available version combinations to make them all works. Here are the versions that I uses

• Gradle: 2.1
• Groovy: 2.3.6
• Ant: 1.9.3
• JVM: 1.6.0_65 (Apple Inc. 20.65-b04-462)
• OS: Mac OS X 10.9.5 x86_64
• Android Studio: 0.8.11 (build AI-135.1446794)
• IntelliJ: IDEA 14 CE EAP, build IC-138.2458.8
• Android gradle plugin: com.android.tools.build:gradle:0.13.0
• Android ADT gradle plugin: com.neenbedankt.gradle.plugins:android-apt:1.4+
• Compile SDK version: 20
• Build tool version: 20.0.0
• Robolectric: 2.3

Known Issues

My current solution isn’t perfect. But for now, I haven’t working solution for them. Hope it could be fixed in the future

• AAR is not supported in Unit Test. (A tricky issue, I’ll explain more in detail later)
• AssertJ-Android is not supported. (Cause by AAR support issue, alternative available.)

Project Structure and configurations

Here are the project structure:

1
2
3
4
5
6
7
8

RootProject
|- settings.gradle
|- build.gradle
|- Launcher
   \- builde.gradle
\- UnitTest
   |- build.gradle
   \- UnitTest.iml

Here are the contents

1

include ':Launcher', ':UnitTest'

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

buildscript {
    repositories {
        mavenCentral()
    }
    dependencies {
        classpath 'com.android.tools.build:gradle:0.13.0'
    }
}
allprojects {
    repositories {
        mavenLocal()
        mavenCentral()
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70

buildscript {
    repositories {
        mavenCentral()
    }
    dependencies {
        classpath 'com.android.tools.build:gradle:0.13.0'
        classpath 'com.neenbedankt.gradle.plugins:android-apt:1.4+'
    }
}
repositories {
    mavenLocal()
    mavenCentral()
}
apply plugin: 'com.android.application'
apply plugin: 'android-apt'
android {
    compileSdkVersion 20
    buildToolsVersion '20.0.0'
    defaultConfig {
        minSdkVersion 9
        targetSdkVersion 19
        versionCode 1
        versionName "1.0"
    }
    buildTypes {
        debug {
            runProguard false
            proguardFiles getDefaultProguardFile('proguard-android.txt'), 'proguard-rules.txt'
        }
        release {
            runProguard false
            proguardFiles getDefaultProguardFile('proguard-android.txt'), 'proguard-rules.txt'
        }
    }
}
apt {
    arguments {
        androidManifestFile variant.processResources.manifestFile
        resourcePackageName 'me.timnew.game.launcher'
    }
}
def AAVersion = '3.1'
dependencies {
    apt "org.androidannotations:androidannotations:$AAVersion"         // Process AA annotations
    /*
    * Android Studio will remove this line if you try to edit project configuration with GUI.
    * It seems it is a bug of Android Studio since it does not understand DSL `apt`
    */
    compile "org.androidannotations:androidannotations-api:$AAVersion" // AA Runtime API. Becareful
    compile 'de.greenrobot:eventbus:2.2.1'
    compile 'org.easytesting:fest-reflect:1.4.1'
    compile 'com.google.guava:guava:18.0'
    compile 'com.koushikdutta.ion:ion:1.3.8'
    compile fileTree(dir: 'libs', include: ['*.jar', '*.aar']) // Well although I mentioned aar here, but it doesn't load correctly.
    compile 'com.android.support:support-v4:20.0.0'
    compile 'com.android.support:support-annotations:20.0.0'
    compile 'com.android.support:appcompat-v7:20.0.0'
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

buildscript {
    repositories {
        mavenCentral()
    }
    dependencies {
        classpath 'com.android.tools.build:gradle:0.13.0'
    }
}
apply plugin: 'java'
repositories {
    mavenLocal()
    maven { url "$System.env.ANDROID_HOME/extras/android/m2repository" } // Fix 'com.android.support:*' package not found issue
    mavenCentral()
}
dependencies {
    def appModule = project(':Launcher')
    compile appModule
    testCompile appModule.android.applicationVariants.toList().first().javaCompile.classpath       // Include classes from main project
    testCompile appModule.android.applicationVariants.toList().first().javaCompile.outputs.files
    testCompile files(appModule.plugins.findPlugin("com.android.application").getBootClasspath())
    testCompile('junit:junit:4.+') {
        exclude module: 'hamcrest-core'                                                            // Exclude problematic 'hamcrest'
    }
    testCompile 'org.robolectric:robolectric:2.3'
    testCompile 'org.mockito:mockito-core:1.9.5'
    testCompile 'org.assertj:assertj-core:1.6.1'
}
tasks.withType(Test) {
    scanForTestClasses = false
    include "**/*Should.class"
    include "**/*Test.class"
    include "**/*Tests.class"
}

Why uses java plug-in instead of android unit test plug-ins

Well, Gradle DSL provides a lot of flexibility to developer. But it also brought a lot complexity to IDE implementation. To figure out project configuration, IDE need to parse and understand the gradle scripts. Not only DSLs provided by gradle but all stuff come with plug-ins. From IDE, this is almost an impossible mission. So IDE need to figure out a way to simplify the process, such as support a subset of DSL.

For Android project, IntelliJ has difficulties to understand the all variations of android unit test plug-ins. So it is not easy to make unit test runnable from IDE. To solve the issue, you either try to teach IDE about the DSL by providing plug-in to IDE, or uses some languages that IDE understood.

I tried some plug-in available today, but none of them works for me. So I decide to use java DSL, which IntelliJ understood natively. As a trade off, since java gradle plugin doesn’t understand Android Library, so it cannot import .aar libries.

Besides I tried all android unit test gradle plugins, I found all of them depends on android gradle plugin. And android plugin depends on AndroidManifest.xml and some other stuff. It is wield to provide an manifest for your unit test.

So as the final solution, I uses java plug-in, avoid using aar in the test.

Why so complicate

Configurate an working Android project isn’t as easy as it sounds. Differ from iOS community, Google isn’t strong-minded as Apple. As a consequence that Android community is fragmented and lack of unified solution. There are tons of solutions available, but you might need to try them one by one to figure out which fits your requirement.

To make your tool chain, dependencies, IDE work together, compatibility is always your enemy. Even Google has to publish Version Compatibility Table to mitigate the pain.

What a mess!!!!!

References posts, plugins or template projects

Here is a list of things that I tried but failed to fit my requirement. List here since it might be helpful to other people.

• Android Gradle App with Robolectric JUnit tests
• tests-app-robolectric-junit template project
• deckard-gradle template project
• android-unit-test gradle plug in
• android-studio-unit-test-plugin android studio/intellij plugin
• robolectric-gradle-plugin
• robolectric-plugin

Trello just created a page to celebrate their user number reaches 5 million. In their celebration page, they introduce an interesting effect, a number of blue squares rotating and falling from the sky.

By inspecting their source code, I extracted the effect implementation from the page.

As you can see, the effect is implemented with Canvas animation. Trello guys created a light weight particle system.

• ConfettiMachine is the particle system controller, which takes the responsibility to create new particles and call draw method on them one by one.
• Particle is the representation of the blue square, it takes the rotation, fading out and rendering.

The source code is extracted for study purpose, all code and credits belongs to Trello guys.

Introduction

Otto is a great Android event bus solution developed by SquareUp guys. These guys extract the event bus related classes from Google’s Guava, and optimized it for Android. Event Bus is a great solution to keep your code away from messy anonymous or internal classes only used for event handling! And Otto’s simplicity and performance makes it used to be the most popular event bus solution in Android development.

Android Annotations, as known as AA, is another great library that makes Android developers’ lives a lot easier. Just annotating the code, AA helps developer handles the most boring or error-proning tasks for you, including binding widgets binding, asynchronous tasks, life time management, etc…

Issue

Otto and AA are the libraries focusing on different aspects. Theoretically speaking, there shouldn’t be any compatibility issue between them. But the reality Otto event is never delivered to AA annotated classes. By inspecting the code with step by step debugging, I found the root cause of the issue is Otto failed to located @Produce and @Subscribe annotated methods in AA generated code.

Analysis

After a few study work, I finally understood what is the reason behind:

For performance consideration, Android Annotations actually does it work during the compilation time instead of Runtime. AA will derive the annotated classes, and generate some code according to the annotations applied. During the runtime, the classes got instantiated is actually the derived classes instead of the original one, although in the code is accessed via the original class as interface.

Here is a simple example:

I have the class ServerListAdapter, which is used to provide data for a grid view.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50

@EBean
public class ServerListAdapter extends AdvBaseAdapter<InetAddress, ServerView> {
    @RootContext
    protected Context context;
    @SystemService
    protected LayoutInflater inflater;
    @Bean
    protected Bus bus;
    public ServerListAdapter() {
        super(new ArrayList<InetAddress>());
    }
    @AfterInject
    protected void afterInject() {
        bus.register(this);
    }
    @Override
    protected ServerView createView(ViewGroup parent) {
        return ServerView_.build(context);
    }
    @Override
    protected ServerView updateView(ServerView itemView, InetAddress item) {
        itemView.update(item);
        return itemView;
    }
    @Subscribe
    public void fetchServerStatus(DiscoveryStatusEvent event) {
        setItems(event.addresses);
    }
    @Subscribe
    public void onServerStatusUpdated(DiscoveryStatusChangedEvent event) {
        switch (event.type) {
            case SERVER_ONLINE:
                getItems().add(event.address);
                break;
            case SERVER_OFFLINE:
                getItems().remove(event.address);
                break;
        }
        notifyDataSetChanged();
    }
}

And this is the derived class generated by AA during the compiling-time:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

public final class ServerListAdapter_
    extends ServerListAdapter
{
    private Context context_;
    private ServerListAdapter_(Context context) {
        context_ = context;
        init_();
    }
    public static ServerListAdapter_ getInstance_(Context context) {
        return new ServerListAdapter_(context);
    }
    private void init_() {
        inflater = ((LayoutInflater) context_.getSystemService(Context.LAYOUT_INFLATER_SERVICE));
        context = context_;
        bus = Bus_.getInstance_(context_);
        afterInject();
    }
    public void rebind(Context context) {
        context_ = context;
        init_();
    }
}

And here is how it is consumed:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

@EFragment(R.layout.fragment_server_list)
public class ServerListFragment extends Fragment {
    @Bean
    protected DiscoveryService discoveryService;
    @Bean
    protected ServerListAdapter adapter;
    @ViewById(R.id.server_list)
    protected GridView serverGridView;
    @AfterViews
    protected void afterViews() {
        serverGridView.setAdapter(adapter);
        discoveryService.start();
    }
    @Override
    public void onDetach() {
        super.onDetach();
        discoveryService.stop();
    }
}

As you can see, in the ServerListFragment, the ServerListAdapter instance injected into bean is actually the instance of ServerListAdapter_. And due to polymorphic, the instance just behaves like a ServerListAdapter instance.

On the other hand, according to the description on Otto’s Home Page:

In order to receive events, a class instance needs to register with the bus.
…
Registering will only find methods on the immediate class type. Unlike the Guava event bus, Otto will not traverse the class hierarchy and add methods from base classes or interfaces that are annotated. This is an explicit design decision to improve performance of the library as well as keep your code simple and unambiguous.

Otto only search annotations in direct class, which is ServerListAdapter_ in instance, and there isn’t any annotation included. As a consequence, all the @Subscribe annotated methods are ignored by com.squareup.otto.AnnotatedHandlerFinder. So the posted events become dead event due to no subscriber found.

Comments

There is rumor that this issue will be fixed in Otto 2.0. But according to the comment from Jake Wharton, Otto’s developer, Otto 2.0 will take forever to release.

In fact Otto 2.0 Repo has been not touched for 2 years already. Although we could check out the code and build Otto 2.0 by ourselves, but it takes efforts. Especially when some bug is found.

Conclusion

Luckily, although Otto turns into “maintenance mode”, the compatibility issue takes forever to resolve. I found a great Otto alternative, EventBus from GreenRobot. A boring name, but great library.

According to EventBus‘s document, it provides richer feature and better performance than Otto.
The most important EventBus is friendly to AndroidAnnoations. They two works well together.

EventBus and Otto Feature Comparison

EventBus and Otto Performance Comparison